逻辑异或（XOR，全称Exclusive OR）是一种基本的二元运算，在计算机科学和数字电路中占据着重要地位。其主要特点在于，逻辑异或运算的结果取决于两个输入值是否不同：当两个输入值相同，结果为0（假）；当两个输入值不同，结果为1（真）。这种简单的逻辑规则在很多领域中被广泛应用，尤其在数据处理和逻辑设计中有着极其重要的作用。

逻辑异或的基本概念

逻辑异或是一种二进制逻辑运算，其符号通常为"⊕"。在布尔代数中，对于两个输入A和B，异或的真值表如下：

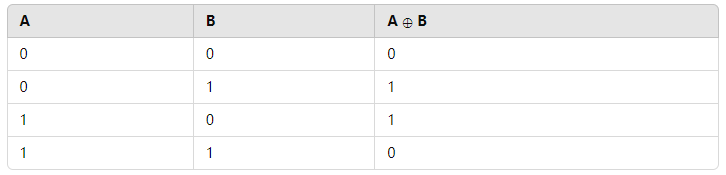
从表格可以看出，异或的运算规则与逻辑与（AND）和逻辑或（OR）有明显的区别。逻辑与要求两个输入值都为真（1）时结果才为真，逻辑或则只需要任意一个输入为真即可。而逻辑异或则强调两个输入值的不一致性，这种特性使其在特定应用中更加高效和实用。

常见的应用场景

逻辑异或的特性使其在许多实际场景中得以广泛应用，以下是几个典型的领域：

1. 数据校验与错误检测

在数据传输过程中，信号可能因噪声或干扰而出错。逻辑异或被广泛用于错误检测和数据校验。例如，在简单的奇偶校验中，通过将数据位进行异或运算，可以快速生成校验位。接收端通过再次执行异或操作，能够快速发现传输数据中是否存在错误，从而提升通信的可靠性。

2. 加密与解密技术

异或运算在加密算法中也有重要应用。最简单的异或加密就是将明文与密钥进行异或运算生成密文。在解密时，使用相同的密钥再次进行异或运算即可还原明文。这种方式计算简单，特别适合对速度要求高的加密场景，如通信加密和简单的数据保护。

3. 逻辑表达式优化与布尔代数简化

在布尔代数中，逻辑异或被用作优化逻辑表达式的重要工具。例如，通过将重复的项进行异或合并，可以简化表达式，从而减少逻辑门的使用量。这种优化方法在数字电路设计中极为重要，有助于提升电路的效率和减少功耗。

4. 编程中的位操作

逻辑异或在程序设计中常被用作一种高效的位操作工具。例如，可以利用异或实现特定位的翻转、清零或设置。一个经典的应用是通过异或交换两个变量的值，而无需额外的临时存储空间：

a = a ⊕ b

b = a ⊕ b

a = a ⊕ b

这种技巧在某些对资源有限的嵌入式系统中尤为实用。

5. 数字电路设计

异或门是数字逻辑设计中重要的基本元件之一。它被广泛应用于奇偶校验生成器、加法器和比较器等功能模块的设计中。例如，在加法器中，异或门用于计算两个位相加后的和位，同时配合逻辑与门计算进位信号，形成完整的加法器结构。

总结

逻辑异或作为一种重要的逻辑运算，凭借其对输入差异性的敏感特性，在数据处理、加密技术、布尔代数、程序设计以及电路设计中表现出了卓越的实用性。无论是简单的数据校验还是复杂的数字电路设计，逻辑异或都不可或缺。它的广泛应用不仅体现了其基础性，更凸显了其逻辑简洁而高效的优势，为现代技术的发展提供了重要支持。